- Теория и практика
Что такое закон Бенфорда: почему маленькие цифры встречаются чаще
Числа в реальной жизни странно себя ведут: чаще всего они начинаются с 1, реже — с 2, и почти никогда — с 9. Это не баг, а закономерность, которую заметили ещё в XIX веке и позже подтвердили на тысячах примеров — от длины рек до финансовой отчётности. Закон Бенфорда помогает находить фальсификации, ошибки и аномалии в данных, и если вы работаете с цифрами — его стоит знать.
История закона Бенфорда начинается не с Фрэнка Бенфорда, а с американского астронома и математика Саймона Ньюкомба. В 1881 году Ньюкомб обратил внимание на интересную особенность: страницы логарифмических таблиц, содержащие числа, начинающиеся с меньших цифр, были заметно более потрепаны, чем страницы с числами, начинающимися с больших цифр. Это навело его на мысль, что в реальных вычислениях люди чаще используют числа, начинающиеся с малых цифр. Ньюкомб опубликовал краткую заметку в American Journal of Mathematics, где предложил формулу для распределения первых значащих цифр, но его наблюдение не привлекло должного внимания и было забыто на полвека.
В 1938 году физик Фрэнк Бенфорд, работавший в исследовательской лаборатории General Electric, независимо переоткрыл эту закономерность. Бенфорд подошел к вопросу более систематично и проанализировал более 20 000 чисел из разнообразных источников: площади рек, списки населения, физические константы, числа в газетных статьях и даже адреса из американских справочников. Его исследование показало, что распределение первых цифр во всех этих наборах данных подчиняется одной и той же закономерности. Бенфорд опубликовал свои результаты в статье «Закон аномальных чисел» в журнале Proceedings of the American Philosophical Society, и с тех пор это статистическое явление стало известно как закон Бенфорда.
Примечательно, что Бенфорд не знал о работе Ньюкомба, и повторное открытие закономерности стало независимым подтверждением её универсальности. Только десятилетия спустя, благодаря работам математика Роджера Пинкхэма в 1961 году и статистика Теда Хилла в 1990-х годах, закон получил строгое математическое обоснование.

Что такое закон Бенфорда?
Закон Бенфорда утверждает, что в многих естественно возникающих наборах числовых данных распределение первой значащей цифры не является равномерным. Вместо этого вероятность того, что первая значащая цифра будет определенным числом, уменьшается логарифмически по мере увеличения этого числа.
Под первой значащей цифрой понимается первая ненулевая цифра в числе. Например, в числе 0,0347 первой значащей цифрой является 3, а в числе 25 789 — цифра 2.
Согласно закону Бенфорда, в естественных наборах данных:
- Цифра 1 встречается как первая значащая примерно в 30,1% случаев
- Цифра 2 — примерно в 17,6% случаев
- Цифра 3 — примерно в 12,5% случаев
- Цифра 9 — всего примерно в 4,6% случаев
Закон применим к данным, которые:
- Охватывают несколько порядков величины
- Не имеют встроенных ограничений или порогов
- Возникают в результате многих независимых процессов
Чтобы стало понятнее: если вы возьмёте список цен на квартиры в городе, метраж домов, бюджетные расходы или даже расстояния между планетами — вы заметите, что около трети всех чисел начинаются с 1, а не с 2, 5 или 9. Это кажется странным, но в данных, которые охватывают разные масштабы и не подчинены искусственным правилам (например, минимальной цене или фиксированному диапазону), такая асимметрия встречается стабильно.
Математическое выражение
Математически закон Бенфорда выражается следующей формулой для вероятности появления цифры d (от 1 до 9) в качестве первой значащей цифры:

Например, вероятность того, что первой цифрой будет 1, вычисляется как: P(1) = log₁₀(1 + 1/1) = log₁₀(2) ≈ 0,301 или примерно 30,1%
Для цифры 9: P(9) = log₁₀(1 + 1/9) = log₁₀(10/9) ≈ 0,046 или примерно 4,6%
Эта формула также может быть записана в виде: P(d) = log₁₀(d + 1) — log₁₀(d)
Важно отметить, что закон Бенфорда можно обобщить и на последующие цифры числа, хотя их распределение постепенно приближается к равномерному по мере удаления от начала числа.
Графическое представление закона Бенфорда демонстрирует характерное убывание частоты появления цифр от 1 к 9. Гистограмма распределения первых цифр по закону Бенфорда имеет следующий вид:
- Цифра 1: 30,1%
- Цифра 2: 17,6%
- Цифра 3: 12,5%
- Цифра 4: 9,7%
- Цифра 5: 7,9%
- Цифра 6: 6,7%
- Цифра 7: 5,8%
- Цифра 8: 5,1%
- Цифра 9: 4,6%
Для сравнения: при равномерном распределении каждая цифра встречалась бы с частотой около 11,1% (поскольку 100% ÷ 9 ≈ 11,1%).
Это распределение часто приводит в недоумение людей, впервые сталкивающихся с законом Бенфорда, так как интуитивно кажется, что все цифры должны встречаться примерно одинаково часто. Однако множество эмпирических исследований и математических доказательств подтверждают универсальность этой закономерности для широкого спектра естественных данных.
Где работает закон Бенфорда?
Закон Бенфорда на первый взгляд может показаться математическим курьезом, однако его проявление в различных наборах данных настолько широко, что позволяет использовать его как практический инструмент анализа. Тем не менее, важно понимать, в каких случаях можно ожидать соответствия закону Бенфорда, а в каких — нет.
Финансовые данные
Финансовая сфера представляет собой классическую область применения закона Бенфорда. Исследования показывают, что следующие наборы данных обычно хорошо соответствуют этому закону:
- Бухгалтерские записи: суммы счетов, проводки, данные о доходах и расходах компаний
- Налоговые декларации: суммы доходов, уплаченных налогов, налоговых вычетов
- Биржевые показатели: объёмы торгов, цены акций, рыночная капитализация
- Микроэкономические данные: цены товаров, объёмы продаж, размеры транзакций
Это делает закон Бенфорда особенно полезным для аудиторов и финансовых аналитиков при поиске потенциальных манипуляций с отчетностью.
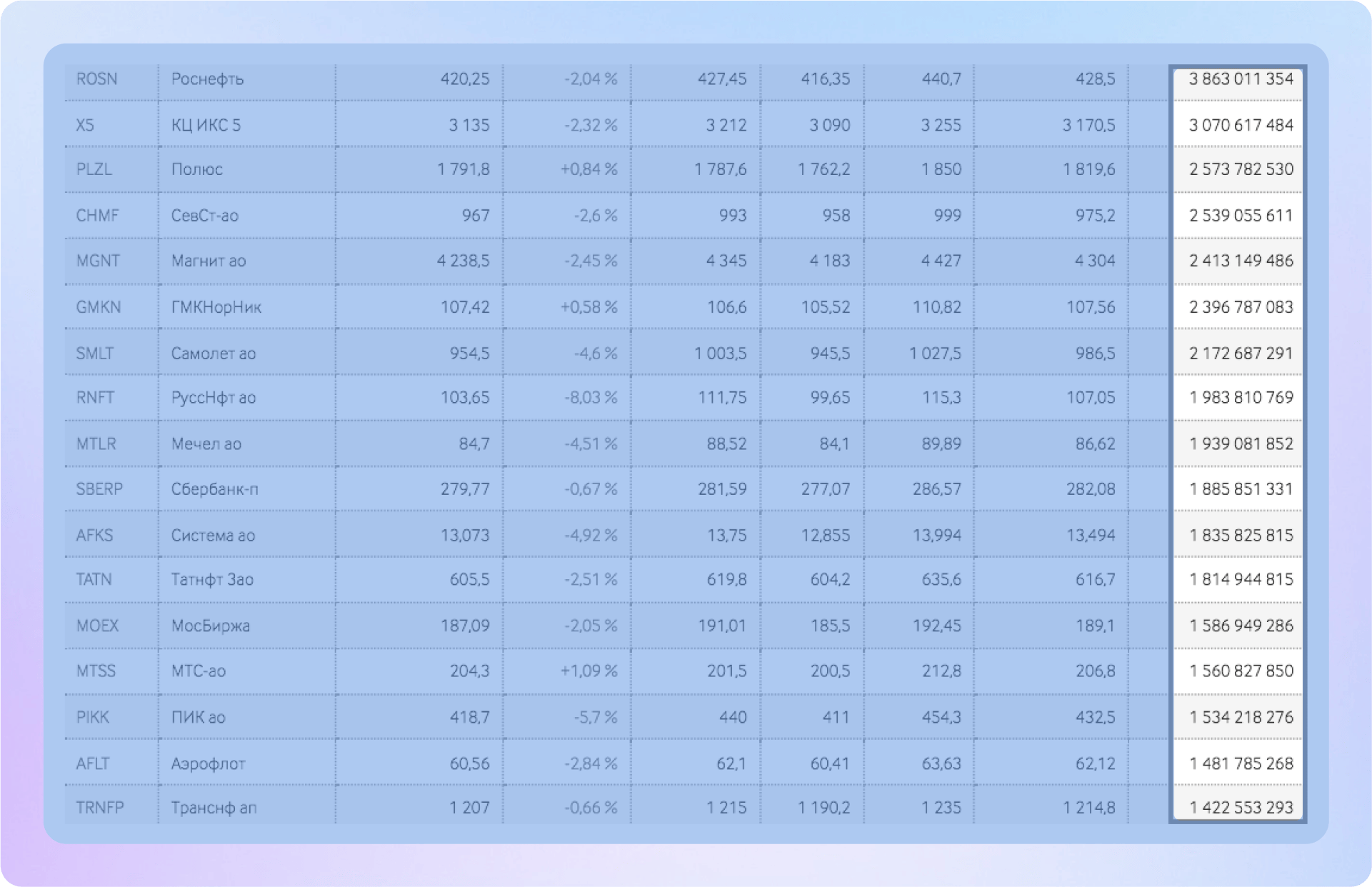
Демографические показатели
Демографические данные также демонстрируют хорошее соответствие закону Бенфорда:
- Численность населения: городов, районов, стран и других административных единиц
- Площади географических объектов: стран, озер, островов, лесных массивов
- Статистика рождаемости и смертности: по регионам, возрастным группам, причинам
- Данные о миграции: объёмы перемещения людей между регионами, странами
Анализ демографических данных на соответствие закону Бенфорда позволяет выявлять потенциальные манипуляции при проведении переписей населения или составлении демографических прогнозов.
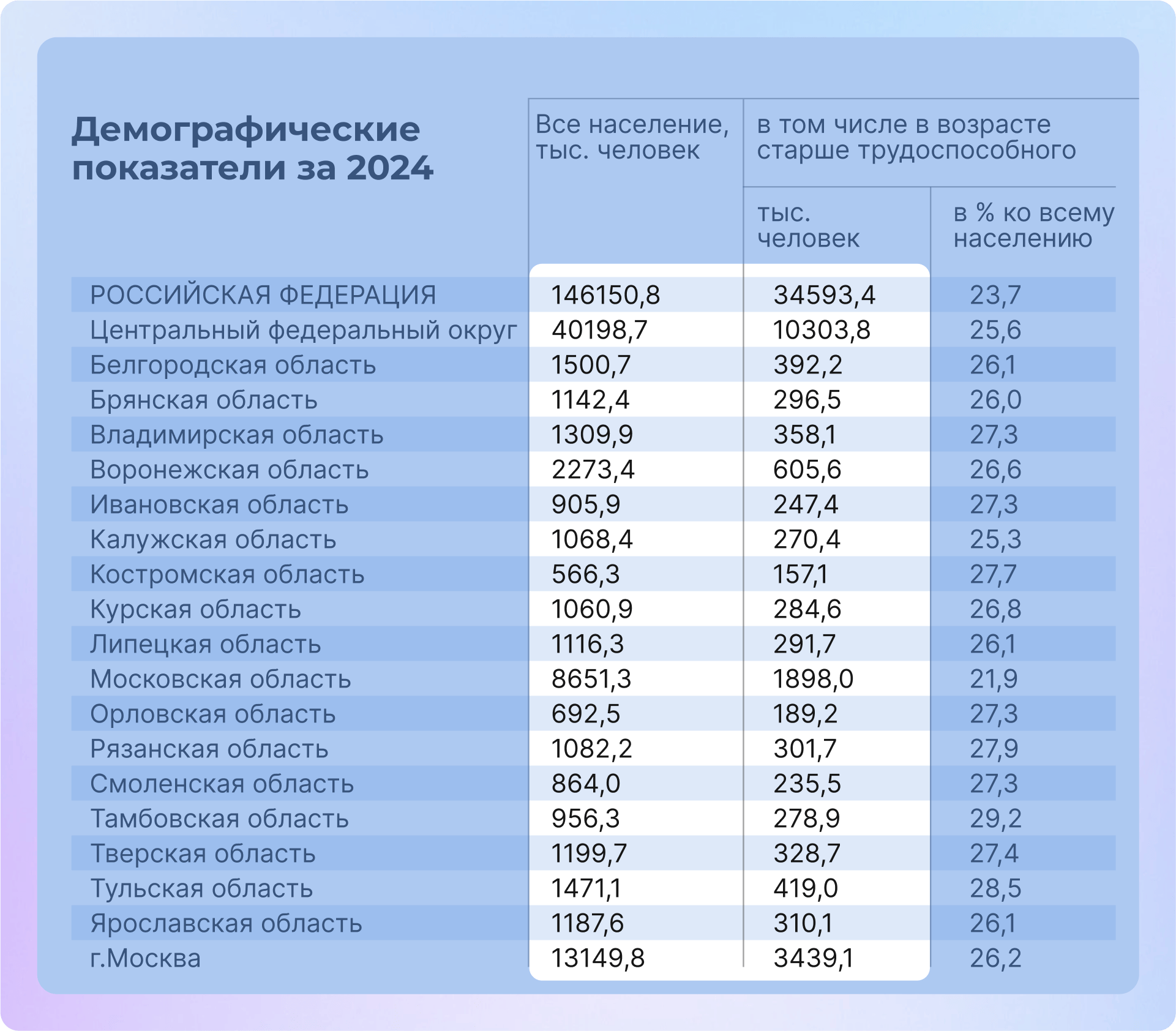
Источник: Росстат
Физические и природные величины
Многие природные и физические измерения также подчиняются закону Бенфорда:
- Гидрологические данные: расход воды в реках, площади водосборных бассейнов
- Геологические измерения: высоты гор, глубины озер, размеры минералов
- Астрономические величины: массы звезд, размеры галактик, расстояния между космическими объектами
- Физические константы и измерения: атомные массы, длины волн, периоды полураспада
Это свойство может использоваться для проверки качества измерений в научных исследованиях.
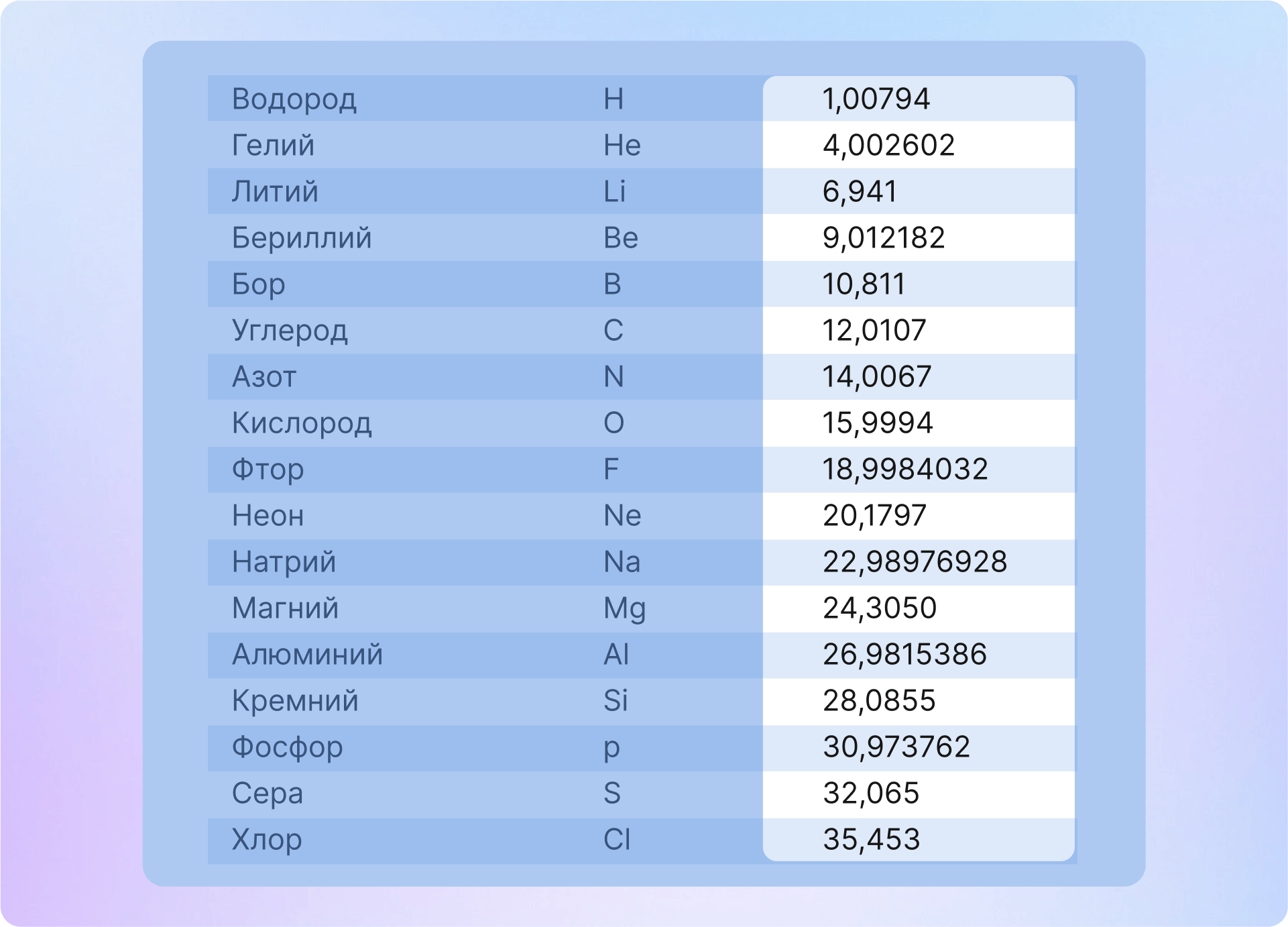
Ограничения применимости
Несмотря на широкую применимость, закон Бенфорда имеет ряд существенных ограничений.
Виды данных, не подчиняющихся закону
Следующие типы данных обычно не соответствуют распределению Бенфорда:
- Телефонные номера: они обычно начинаются с определённых цифр согласно правилам нумерации и имеют искусственно заданную структуру
- Персональные идентификаторы: номера паспортов, страховых полисов, ИНН и другие идентификаторы, генерируемые по специальным алгоритмам
- Почтовые индексы: распределение зависит от административного деления, а не естественных процессов
- Даты: ограничены диапазоном (1–31 для дней, 1–12 для месяцев), что не позволяет проявиться логарифмическому распределению
- Лотерейные номера: если они действительно случайны, то должны иметь равномерное распределение первых цифр
Условия, при которых закон перестает работать
Закон Бенфорда перестает быть применимым в следующих условиях:
- Узкий диапазон значений: данные, которые не охватывают несколько порядков величины (например, рост взрослых людей, который варьируется в узком диапазоне от примерно 1,5 до 2,1 метра)
- Наличие минимальных или максимальных значений: искусственные пороги или ограничения (например, зарплаты, не ниже минимального размера оплаты труда)
- Присвоенные номера: последовательно пронумерованные объекты (например, номера домов на улице)
- Психологически сформированные числа: цены, заканчивающиеся на 9 или 99 (например, 19,99), которые устанавливаются с учетом маркетинговых соображений
- Очень малые выборки: при небольшом количестве данных (менее 100-200 наблюдений) могут наблюдаться существенные отклонения от закона
Искусственно созданные наборы данных
Особую категорию представляют искусственно генерируемые данные:
- Случайные числа: при истинно случайной генерации первые цифры должны иметь равномерное распределение, а не распределение Бенфорда
- Придуманные людьми числа: когда людей просят «придумать случайное число», они часто не соблюдают закон Бенфорда, что используется для выявления фальсифицированных данных
- Данные, созданные по определенным формулам: могут соответствовать или не соответствовать закону в зависимости от характеристик формулы
- Симулированные данные: в компьютерных моделях соответствие закону Бенфорда зависит от алгоритмов генерации
Понимание границ применимости закона Бенфорда критически важно при его использовании для анализа данных и выявления аномалий. Неверная интерпретация может привести как к ложным обвинениям в манипуляции данными, так и к пропуску реальных случаев фальсификации.
Практическое применение закона Бенфорда
Закон Бенфорда перешел из разряда математических курьезов в категорию практических инструментов благодаря своей способности выявлять аномалии в наборах данных. Сегодня этот закон используется специалистами различных областей — от финансовых аудиторов до судебных экспертов и научных исследователей. Рассмотрим основные направления его практического применения.
Анализ финансовой отчетности
Одно из самых распространенных применений закона Бенфорда — проверка финансовой отчетности компаний. Когда бухгалтеры или финансисты фальсифицируют данные, они обычно не учитывают естественное распределение первых цифр, что создает заметные отклонения от закона Бенфорда.
Финансовые аналитики используют следующие подходы:
- Проверка распределения первых цифр в балансовых отчетах
- Анализ журналов проводок на соответствие закону Бенфорда
- Мониторинг изменений в распределении первых цифр по кварталам или годам
- Сравнение распределений в разных подразделениях одной компании
Например, исследование, проведенное профессором Марком Нигрини, показало, что компания Enron демонстрировала существенные отклонения от закона Бенфорда в квартальных отчетах задолго до того, как ее мошеннические схемы были раскрыты другими методами.
Выявление налоговых махинаций
Налоговые органы по всему миру используют закон Бенфорда как инструмент предварительного скрининга при выборе объектов для детальных проверок:
- Анализ распределения первых цифр в налоговых декларациях физических лиц
- Проверка отчетов о доходах и расходах предприятий
- Исследование данных о налоговых вычетах и льготах
- Выявление подозрительных шаблонов в отчетности групп налогоплательщиков
В Италии, например, налоговая служба использовала анализ на соответствие закону Бенфорда для выявления компаний с высоким риском налоговых нарушений. Это позволило более эффективно распределять ресурсы при проведении аудиторских проверок.
Аудит и проверка достоверности данных
Аудиторские компании интегрировали проверку на соответствие закону Бенфорда в свои стандартные процедуры:
- Первичный скрининг финансовых данных перед детальным аудитом
- Автоматизированный мониторинг транзакций в реальном времени
- Выявление подозрительных шаблонов в счетах, выставляемых поставщиками
- Проверка инвентаризационных списков и отчетов о движении товаров
Международные стандарты аудита (МСА) рекомендуют использование аналитических процедур, включая тесты на соответствие закону Бенфорда, как часть оценки рисков существенного искажения финансовой отчетности.
Методы проверки качества данных
За пределами выявления мошенничества закон Бенфорда используется для общей оценки качества данных:
- Оценка полноты собранной информации
- Выявление возможных ошибок при сборе или вводе данных
- Проверка корректности агрегирования информации
- Валидация данных, полученных из разных источников
Специалисты по обработке данных используют отклонения от закона Бенфорда как сигнал о необходимости более тщательной проверки набора данных, что позволяет выявлять проблемы еще до начала основного анализа.
Выявление аномалий и выбросов в наборах данных
Закон Бенфорда эффективен для выявления необычных паттернов в данных:
- Обнаружение аномальных выбросов в больших массивах информации
- Идентификация подозрительных кластеров значений
- Определение границ между естественными и искусственными данными
- Автоматизированный скрининг больших массивов данных для дальнейшего экспертного анализа
Например, в экологических исследованиях анализ на соответствие закону Бенфорда помогает выявлять участки с аномальными показателями загрязнения, которые требуют дополнительного изучения.
Оценка достоверности статистических исследований
Научное сообщество использует закон Бенфорда для оценки добросовестности исследований:
- Проверка экспериментальных данных на признаки манипуляций
- Анализ опубликованных результатов исследований
- Выявление потенциально сфабрикованных или «украшенных» данных
- Оценка достоверности статистических выборок
В 2011 году группа исследователей применила анализ на соответствие закону Бенфорда для проверки опубликованных научных статей по психологии и выявила статистически значимые отклонения в работах некоторых авторов, что позднее привело к отзыву ряда публикаций.
Часто задаваемые вопросы (FAQ)
Почему первые цифры вообще подчиняются какому-то закону?
Потому что так работает мир. Многие процессы в природе растут не линейно, а экспоненциально — чем больше величина, тем быстрее она увеличивается. А при таком росте числа чаще «задерживаются» на первой цифре 1, чем на 9. Пример: чтобы вырасти с 1 до 2 млн — нужно удвоиться. А чтобы вырасти с 5 до 6 — всего +20%.
Плюс — масштаб не важен. Считайте в метрах, дюймах, долларах или евро — распределение первых цифр будет тем же. Это называется инвариантностью к масштабу.
А если углубиться в математику: при перемножении случайных величин мы получаем логнормальное распределение. А оно как раз и даёт Бенфордовское распределение первых цифр.
Можно ли подделать данные так, чтобы они прошли проверку по закону Бенфорда?
Можно. Но сложно. Честно сгенерировать фальшивые данные под закон Бенфорда — это почти как подделать почерк под микроскопом:
- Придётся вручную или программно подгонять каждое число под нужную первую цифру.
- Набор данных будет выглядеть правдоподобно только снаружи.
- А внутри — следы: нарушенные связи между цифрами, подозрительные комбинации, аномалии в других тестах.
Аудиторы это знают. Поэтому проверяют не только первую цифру, но и вторую, и последнюю, и связи между числами. Один закон — не защита. Вся система — защита.
Если данные соответствуют закону Бенфорда — значит, они настоящие?
Нет. Соответствие — это индикатор, а не доказательство.
- Иногда настоящие данные не попадают под закон: если выборка маленькая, или если есть естественные ограничения (например, зарплаты не бывают ниже МРОТ).
- Иногда подделка может пройти тест — если её аккуратно нарисовали.
- И всегда важен контекст: в одних областях отклонение в 5% — это норма, в других — тревожный сигнал.
Закон Бенфорда — это повод копнуть глубже, а не выносить приговор. Его используют как фильтр, а не как штамп.
Какие ещё закономерности есть в цифрах?
Бенфорд — не единственный. Вот другие:
- Закон Зипфа — частые слова и числа встречаются чаще, чем редкие, и делают это по строго убывающей логике.
- Принцип Парето (80/20) — 20% причин дают 80% результатов. Часто срабатывает
- Закон Хика — чем больше вариантов, тем дольше думаем.
- Закон округления — люди любят «красивые» числа: 10, 100, 500. И это видно в данных.
- Левенштейн — мера отличия между строками. Полезно для поиска ошибок в текстах и цифрах.
- Закон Лотки — в науке: мало кто пишет много статей, много кто — по одной.
Всё это — инструменты, которые помогают находить аномалии и понимать, как устроены данные.